علماء الرياضيات يعثرون على رقم جديد بعد 32 عاما من البحث

بعد نحو 32 سنة من البحث، وبمساعدة كمبيوتر فائق السرعة، اكتشف علماء الرياضيات أخيرًا مثالًا جديدًا لعدد صحيح خاص يسمى رقم ديديكيند.

الرقم الجديد هو التاسع من نوعه، ويسمى D(9)، ويحتسب على أنه يساوي 286 386 577 668 298 411 128 469 151 667 598 498 812 366، وهو يتبع الرقم D(8) المكون من 23 رقمًا والذي تم اكتشافه في عام 1991.

استيعاب مفهوم عدد ديديكيند أمر صعب لغير علماء الرياضيات، ناهيك عن حله. في الواقع، الحسابات المعنية معقدة للغاية وتتضمن أعدادًا ضخمة جدًا، ولم يكن من المؤكد أنه سيتم اكتشاف D(9) على الإطلاق.

وقال عالم الكمبيوتر لينارت فان هيرتوم، من جامعة بادربورن في ألمانيا: "على مدار 32 سنة، كان حساب D(9) يمثل تحديًا مفتوحًا، وكان من المشكوك فيه ما إذا كان من الممكن حساب هذا الرقم على الإطلاق".

في مركز رقم ديديكيند توجد دوال منطقية، أو نوع من المنطق الذي يختار مخرجات من المدخلات المكونة من حالتين فقط، مثل صحيح وخطأ، أو 0 و1.

الوظائف البوليانية الرتيبة هي تلك التي تقيد المنطق بطريقة تجعل تبديل 0 بـ 1 في المدخلات يؤدي فقط إلى تغيير الإخراج من 0 إلى 1، وليس من 1 إلى 0.

يصفها الباحثون باستخدام اللونين الأحمر والأبيض بدلاً من 1 و0، لكن الفكرة هي نفسها.

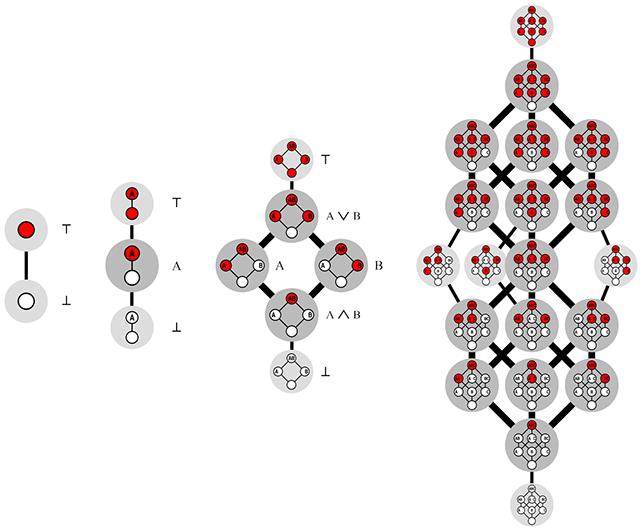
قال فان هيرتوم: "في الأساس، يمكنك التفكير في دالة منطقية رتيبة ذات أبعاد ثنائية وثلاثية ولا نهائية باعتبارها لعبة بمكعب ذي عدد n من الأبعاد".

"يمكنك موازنة المكعب في إحدى الزوايا ثم تلوين كل زاوية من الزوايا المتبقية إما باللون الأبيض أو الأحمر".

هناك قاعدة واحدة فقط: يجب ألا تضع أبدًا زاوية بيضاء فوق زاوية حمراء. وهذا يخلق نوعًا من التقاطع العمودي بين الأحمر والأبيض. والهدف من اللعبة هو حساب عدد القطع المختلفة الموجودة.

يحسب علماء الرياضيات D(1) على أنه 2 فقط، ثم 3، 6، 20، 168...

في عام 1991، استغرق الأمر حاسوبًا عملاقًا من نوع Cray-2 (أحد أقوى الحواسيب العملاقة في ذلك الوقت) وعالم الرياضيات دوج فيدمان 200 ساعة لمعرفة D(8).

انتهى الأمر بـ D(9) ليصبح طوله ضعف طول D(8) تقريبًا، ويتطلب نوعًا خاصًا من الكمبيوتر العملاق: جهاز يستخدم وحدات متخصصة تسمى مصفوفات البوابة القابلة للبرمجة الميدانية (FPGAs) والتي يمكنها إجراء حسابات متعددة بالتوازي.

يقول عالم الكمبيوتر كريستيان بليسل، رئيس مركز بادربورن للحوسبة المتوازية (PC2): "يعد حل المشكلات التوافقية الصعبة باستخدام FPGAs مجالًا واعدًا للتطبيق، ويعد Noctua 2 واحدًا من أجهزة الكمبيوتر العملاقة القليلة في جميع أنحاء العالم التي يمكن إجراء التجربة عليها على الإطلاق".

كانت هناك حاجة إلى مزيد من التحسينات لمنح Noctua 2 شيئًا للعمل معه. باستخدام التماثلات في الصيغة لجعل العملية أكثر كفاءة، أعطى الباحثون الكمبيوتر العملاق مبلغًا ضخمًا لمعرفة ذلك، وهو مجموع يتضمن 5.5*10^18 حدًا (يقدر عدد حبات الرمل على الأرض بـ 7.5*10^18 للمقارنة).

وبعد 5 أشهر، توصل Noctua 2 إلى الإجابة، ولدينا الآن D(9). لم يقم الباحثون بالإشارة إلى D(10) في الوقت الحالي، ولكن يمكننا أن نتخيل أن الأمر قد يستغرق 32 عامًا أخرى للعثور عليه، حسب موقع سايتس ألرت.